رسم پلات سه بعدی در متلب

در ادامه آموزش های سایت همیارپروژه برنامه نویسی متلب ارائه خواهد شد .آموزشها از مقدماتی تا پیشرفته ادامه دارد و ما به شما کدنویسی در نرم افزار متلب را یاد خواهیم داد. با ما همراه باشید.

بدست آوردن یک نقشه ی کانتور رنگی هاشور خورده از تابع contourf و تابع  colorbar در متلب مطابق زیر استفاده خواهیم کرد:

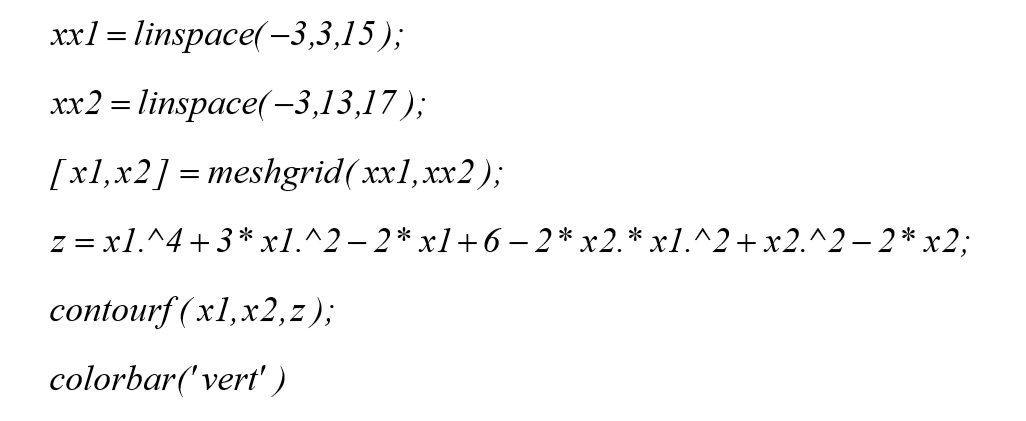
که در آن vert در تابعcolorbar جهت تعیین شیوه ی نمایش به صورت ستونی بکار رفته است. اجرای این برنامه نتایج نشان داده شده در شکل زیر را نمایش خواهد داد.

کاربر همچنین می تواند با استفاده از دستور

Cylinder

از منحنی های دو بعدی به عنوان مولدی برای ایجاد سطوح احجام دوران داده شده استفاده نماید . جهت روشن تر شده موضوع در نرم افزار متلب منحنی زیر را در نظر بگیرید:

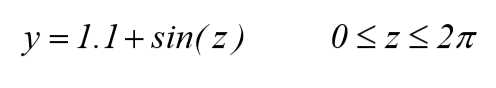
این منحنی حول محور Z به اندازه ی ۳۶۰° چرخیده است. برنامه بصورت زیر می باشد:

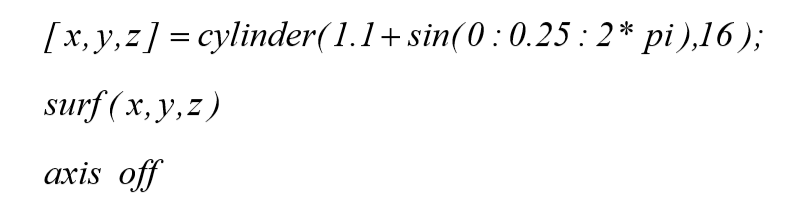
که پس از اجرای کد فوق در متلب تصویر زیر نمایش داده می شود.

در شکل فوق , زاویه های دید, مقدارهای پیش فرض می باشند. مواردی وجود دارد که کاربر تمایل به تغییر زوایای دید پیش فرض بدلیل قسمتهایی از سطح که مورد نظر هستند, دیده نمی شوند. نشان دادن چند نمای مختلف از سطح با استفاده از تابع subplot مطلوب می باشد.

کاربر بخواهد قبل از تصمیم گیری در مورد نمای قطعی , نماهای مختلف شکل را مشاهده کند. نرم افزار متلب دارای روشی مستقیم با استفاده از توابع rotate3d و view جهت تعیین نماهای دید در متلب می باشد.

در شکل زیر زوایای دید به شیوه ی زیر تعیین شده اند. در پنجره ی فرمان نرم افزار متلب عبارت rotate3d تایپ می شود و یا آیکن rotate در پنجره ی شکل کلیک می شود. که اینکار کلیک چپ ماوس را فعال خواهد کرد. در پنجره ی فرمان متلب , کلیک چپ ماوس فشرده شده و تا هنگامی که محورها به موقعیت جدیدی که نمای شکل بهتر شود, انتقال یابند, فشرده می ماند. سپس کلیک ماوس رها شده و ترسیم سه بعدی ایجاد می شود.

اگر نما, رضایت بخش نباشد, در اینصورت این روند تا هنگامیکه نمای مناسبی ایجاد شود, ادامه خواهد یافت. پس از اینکه نمای مناسبی بدست آمد, به پنجره ی فرمان متلب باز گشته و عبارت:

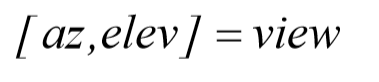
را تایپ کنید. در اینصورت دو عدد نمایش داده می شوند. عدد اول برای az و عدد دوم برای elev ( هر نام دیگری را می توان برای متغیر ها به کار برد) می باشد.

کاربر پس از تابع ایجاد سطح در برنامه,

View(n,m)

را وارد می کند. که در آن, مقدار عددی برای متلب az و m , مقدار عددی برای elev می باشد. با انجام موارد فوق مقادیر az=-35.5 و elev=-34 بدست خواهند آمد. بنابراین برنامه ی اصلاح شده, به صورت زیر خواهد بود:

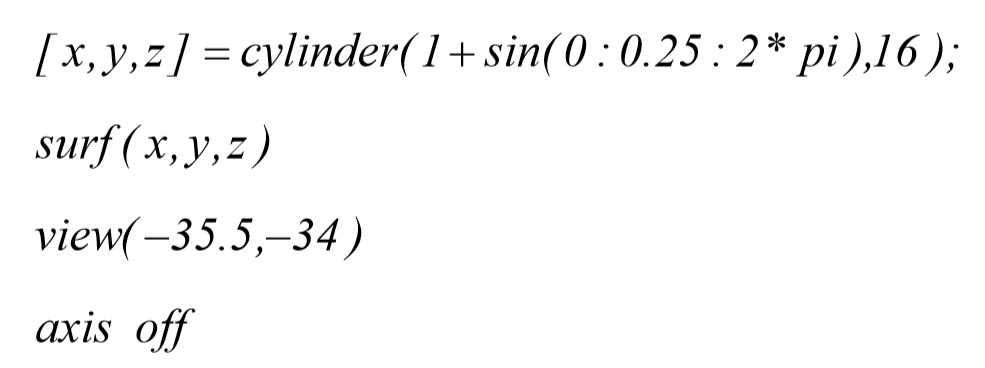
که پس از اجرای برنامه در متلب شکل زیر نمایش داده می شود:

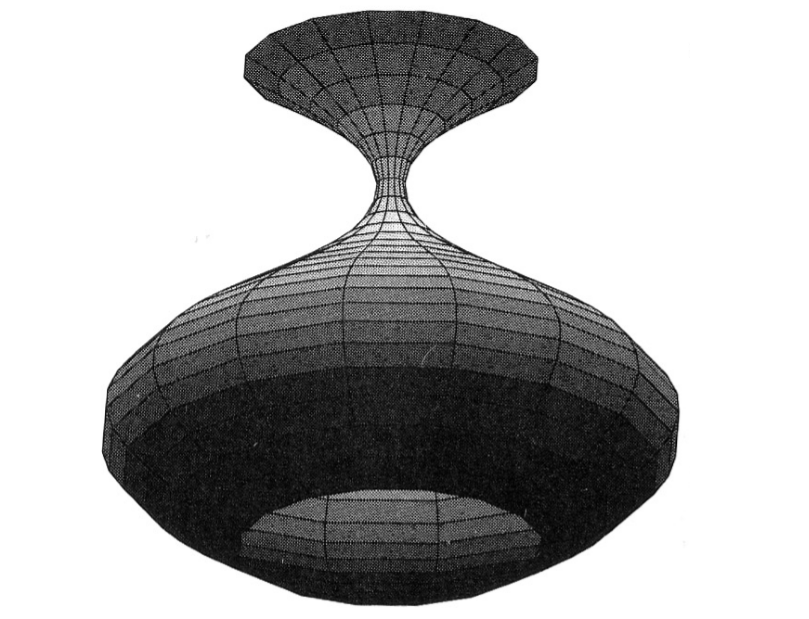
همچنین می توان چندین سطح را در یک شکل از متلب ایجاد نمود. سطح زیر به معادله ی مورد نظر در بازهی آن:

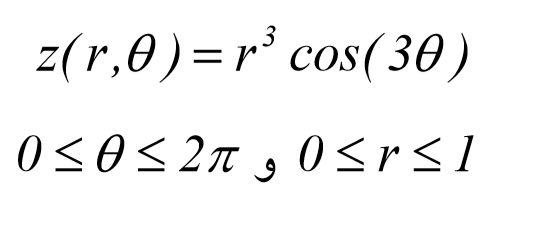
فرض می شود که این سطح دو دیسک ب شعاع L را که در z=10.5 واقعند, قطع می کند. برنامه ی ایجاد این سطوح به صورت زیر می باشد.

که پس از اجرا نمودن کد فوق در متلب تصویر زیر نمایش داده می شود:

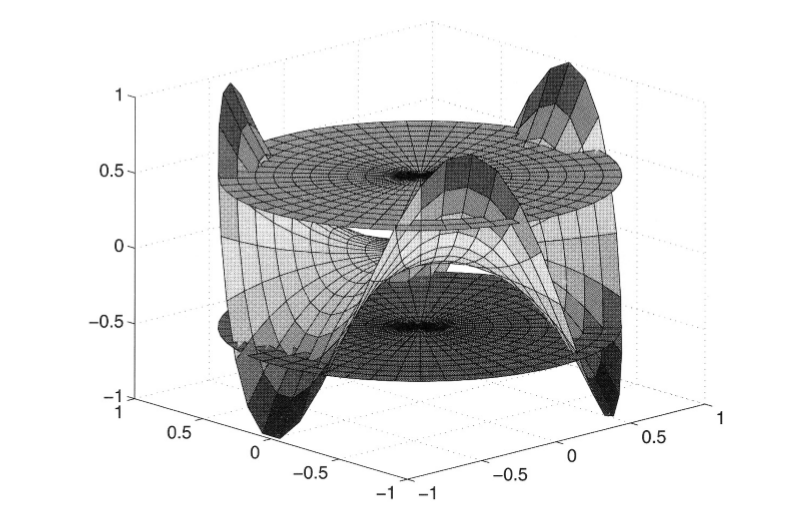
ایجاد صفحات در متلب

فرض نمایید سه نقطه ی

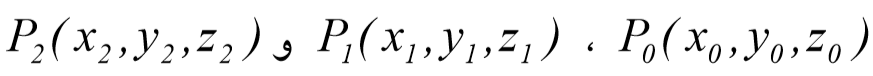
در فضا مشخص شده باشد. نمایش پارامتریک هر نقطه ای در صفحه ی شامل این نقاط توسط رابطه ی زیر در متلب تعیین می گردد.

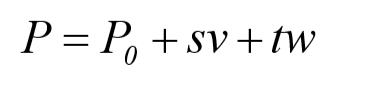
که در آن داریم:

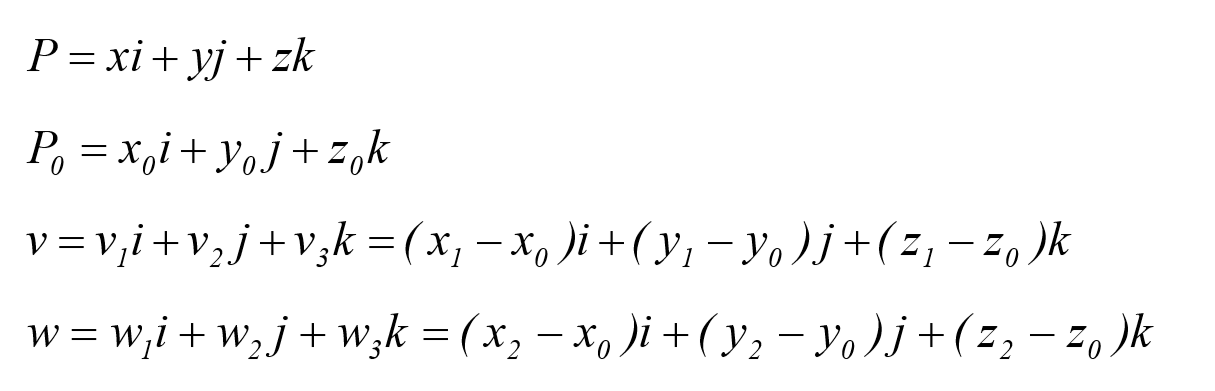
و داریم:

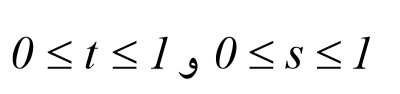
بنابراین:

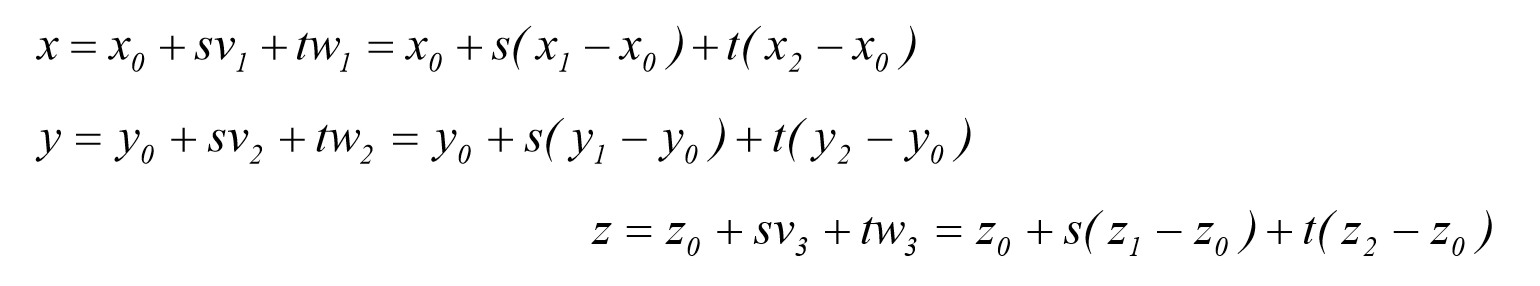
خواهد بود. اگر فرض شود که می توان صفحه را بصورت سطحی متشکل از شبکه ای ۵*۵ از قطعات در نظر گرفت. ما می توانیم تابعی با نام Planarsurface جهت ایجاد و نمایش سطح صفحه ای ایجاد کنیم.

که در آن P0 , P1 و P2 هر یک بردارهایی سه عنصره شامل مختصه های نقاط روی صفحه می باشند. بنابراین با وارد کردن عبارت زیر در چنجره ی فرمان متلب :

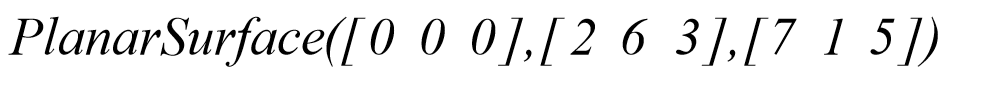
نتایج بدست آمده همانند شکل زیر خواهد بود:

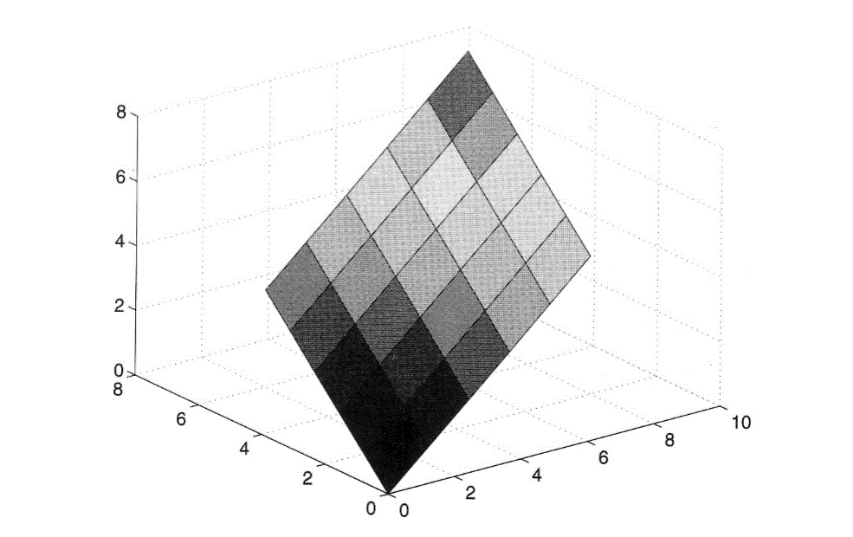
جهت تصویر کردن سطح روی سه صفحه ی اصلی عمود بر هم , از علامت ضرب نقطه ای استفاده می کنیم. لذا برای تصویر نمودن سطح روی صفحه ی xy در متلب داریم:

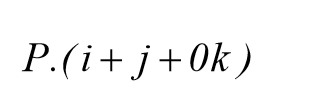
که معادل با مینیمم کردن مختصه های Z نقاط روی صفحه می باشد. بطور مشابه برای تصویر کردن سطح روی صفحه ی yz داریم:

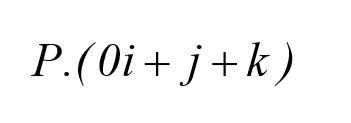
که معادل با مینیمم کردن مختصه های X نقاط روی صفحه می باشد. جهت تصویر کردن سطح روی صفحه ی XZ در متلب داریم:

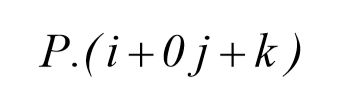
که معادل با مینیمم کردن مختصه های y نقاط روی صفحه می باشد. لذا می توان تابع Surfaceplaner را بگونه ای اصلاح کرد, که شامل گزینه ای اختیاری جهت نمایش این تصاویر باشد.

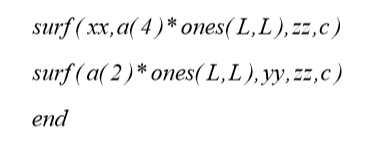
که در آن Projection می تواند هر عددی باشد. آرایه ی C بگونه ای تعریف می شود که تصاویر به رنگ زرد نمایش داده می شوند. دو اندیس اول آرایه ی C باید دارای مرتبه ی یکسان با xx , yy و zz باشند. اندیس آخری باید دقیقا سه عنصر را نشان بدهد, که هر یک می توانند دارای مقدار ی بین ۰ و ۱ باشد. این سه عنصر اخری رنگ هر قطعه را در هر ترکیبی از دو اندیس اول تعیین می کنند. اگر عبارت زیر را در پنجره ی فرمان نرم افزار متلب وارد می نماییم.

بنابراین شکل زیر را خواهیم داشت.

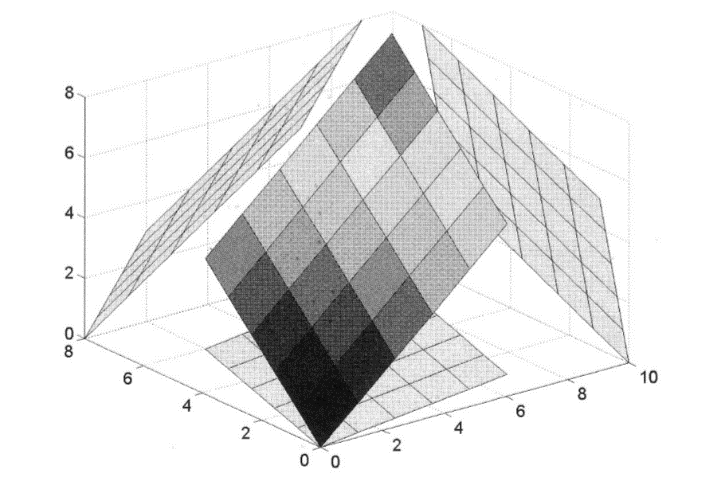
اگر چه تصور می رود که تصاویر, در صفحات مورد نظر تصویر نشده اند. اما استفاده از تابع rotate3d ما را از این بابت مطمئن می سازد.

 

در اینجا آشنایی با محیط متلب بخش هشتاد و سوم به پایان رسیده است و در آموزش های بعدی به مباحث دیگر آموزش متلب می پردازیم. همچنین از شما مخاطبین عزیز سایت همیارپروژه دعوت می کنم که برای انجام پروژه متلب خود آموزش های ما را دنبال نمایید.

 

نویسنده: زهرا رستمی