شبکه‌های آدلاین و یادگیری LMS در متلب

در ادامه آموزش های سایت همیارپروژه برنامه نویسی متلب ارائه خواهد شد .آموزشها از مقدماتی تا پیشرفته ادامه دارد و ما به شما کدنویسی در نرم افزار متلب را رایگان یاد خواهیم داد. با ما همراه باشید.

شبکه های آدلاین و یادگیریLMS در متلب

.شبکه آدلاین با قانون یادگیری ویدرو-هوف (معروف به قانون LMS ) در سال ۱۹۶۰ و بعد از شبکه پرسپترون با قانون یادگیری SLPR به وجود آمد.

. شبکه آدلاین شبیه پرسپترون اشت وای با تابع تبدیل خطی (به جای آستانه دومقداره) .

.محدودیت شبکه‌های پرسپترون و آدلاین:

_فقط توانایی طبقه بندی الگوهایی را دارند که به طور خطی از هم جداپزیرند.

قانون SLPR در متلب

_همگرایی به یک جواب را در صورت وجود تضمین می‌کند.

_ نسبت به نویز خیلی حساس است، زیرا خط مرزی خیلی نزریک الگوهای یادگیری است.

 قانون LMS در متلب

_خیلی قویتر از SLPR

_ دارای کاربرد های فراوان در مهندسی و بخصوص پردازش سیگنال.

شبکه آدلاین در متلب

_مناسب برای تقریب خطی یک تابع یا اجرای عمل شناسایی الگو.

_دارای منحنی سطح خطای اجرایی سهموی.

_دارای مزیت برخورداری از یک نقطه مینیمم.

_یادگیری از نوع با ناظر.

پارامترهای شبکه به نحوی تنظیم می شوند که شاخص اجرای میانگین مربعات خطا بهینه شود.

_قانون یادگیری LMS تقریبی از الگووریتم بیشترین شیب در حداقل کردن شاخص اجرایی.

_حتی در صورت عدم اجرای جواب (در این حالت قانون SLPR همگرا نخواهد شد) باز به جای میانگین مربعات خطا حداقل است، همگرا می شود.

_نسبت به نویز کمتر حساس.

مبانی بهینه سازی و نقاط بهینه در متلب

. پایه همه تکنیک های یادگیری از نوع عملکردی

. در یادگیری عملکردی پارامترهای شبکه به نحوی تنظیم می شوند که عملکرد شبکه بهینه شود.

. قدم اول : تعیین عملکرد و تعیین شاخص عملکرد. (معمولا سطح اجرایی میانگین مربعات خطا )

. قدم دوم : جستجو در فضای پارامترهای شبکه برای تنظیم آنها به طوریکه معیار اجرایی عملکرد کاهش یابد.

. بسط تیلور تابع (X)F با متغیر برداری X .

. برادران گرادیان و ماتریس هسیان تابع F به ترتیب برابرند با :

مبانی بهینه سازی: مشتقات برداری جهت دار در متلب

. مشتق تابع F در مسیر بردار P :

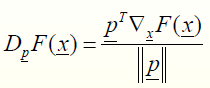
. مشتق تابع F در مسیر بردار P :

سوال:

در چه مسیرهایی مقدار مشتق برداری ماکزیمم، مینیمم یا صفر خواهد بود؟

. برای اینکه X نقطه مینیمم تابع F باشد

_ شرط درجه اول :

نقاط ایستای تابع f در متلب

_ شرط درجه دوم: (ماتریس مثبت معین)

. شرط لازم برای نقطه مینیمم X :

.شروط لازم و کافی برای نقطه مینیمم  X :

. شرط کافی برای اینکه X زین اسبس باشد، ماتریس هسیان نامعین باشد.

مبانی بهینه سازی:توابع درجه دوم

.متقارن بودن A الزامی نیست زیرا هردو ماتریس نامتقارن را می توان به متقارن جدید تبدیل کرد. چگونه ؟

. شاخص عملکردی میانگین مربعات خطا از نوع مربعات خطا از نوع درجه دوم می باشد.

. تمامی تابع با مشتقات پیوسته مرتبه دوم حول یک ناحیه به اندازه کافی کوچک مثل تابع درجه دوم عمل می کند. چرا ؟

. بیشترین الگوریتم های بهینه سازی با تابع عملکرد مرتبه دوم پس از تعداد محدودی تکرار به نقطه بهینه خواهند رسید.

مبانی بهینه سازی: توابع درجه دوم (مقادیر و بردارهای ویژه) ماتریس هسیان نقش مهمی در مینیمم کردن توابع دارند.

. به علاوه مقادیر و بردارهای ویژه دارای تعابیر فیزیکی نیز هستند.

در اینجا آشنایی با محیط متلب بخش صد و دوم به پایان رسیده است و در آموزش های بعدی به مباحث دیگر آموزش متلب می پردازیم. همچنین از شما مخاطبین عزیز سایت همیارپروژه دعوت می کنم که برای انجام پروژه متلب خود آموزش های ما را دنبال نمایید.

نویسنده: زهرا رستمی

جهت سفارش پروژه به لینک زیر مراجعه نمایید :

سفارش پروژه

همچنین می توانید برای ارتباط سریعتر با شماره و آیدی تلگرام زیر تماس حاصل کنید :
۰۹۱۲۹۵۴۰۱۲۲ – آیدی تلگرام : @fnalk

از طریق کلیک برروی آیکن های زیر میتوانید پروژه خود را در تلگرام و یا واتساپ برای ما ارسال کنید:

ثبت سفارش در واتس آپ ثبت سفارش در تلگرام