آشنایی با محیط Matlab

در ادامه آموزش های سایت همیارپروژه برنامه نویسی متلب ارائه خواهد شد .آموزشها از مقدماتی تا پیشرفته ادامه دارد و ما به شما کدنویسی در نرم افزار متلب را یاد خواهیم داد. با ما همراه باشید.

پردازش سیگنال دیجیتال –توابع fft  و ifft

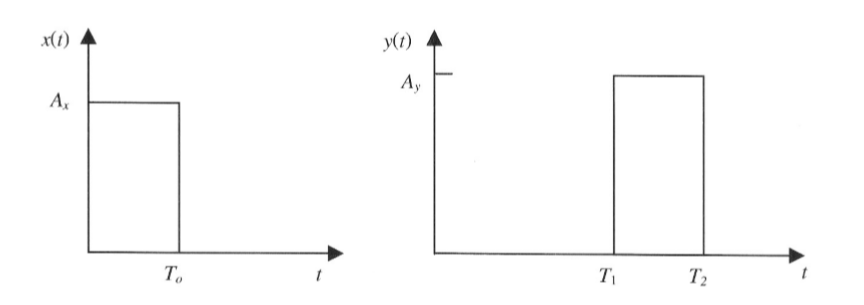
در انجام پروژه پردازش تصویر در متلب از ین کدها استفاده می نماییم. شکل موج زیر را در نظر بگیرید:

تبدیل فوریه گسسسته در نرم افزار متلب

تبدیل فوریه تابع حقیقی g(t) که با فواصل Δt در بازه ی زیر مقدار دهی می شود

می تواند توسط تبدیل فوریه ی گسسته ی زیر تقریب زده شود

که در تبدیل فوریه در متلب مقادیر به صورت زیر تعریف می شود

دقت نمایید که  N  تعداد نمونه ها می باشد. به طور کلی Gn یک کمیت مرکب می باشد . محدودیت موجود در مورد Δt به صورت زیر در متلب اعمال می شود.

 

که در آن fh بالاترین فرکانس g(t) می باشد دقت نمایید که کمیت Gn دارای واحد دامنه- ثانیه و یا دامنه بر هرتز می باشد. تبدیل فوریه معکوس در متلب توسط رابطه ی زیر محاسبه می گردد:

رابطه تبدیل فوریه معکوس

متناظر با مقادیر Gn در فرکانسهای متناظر nΔf کاربر می تواند Gn را در Δf ضرب نماید بنابراین :

لذا داریم:

متوسط توان سیگنال در متلب:

جهت محاسبه پاسخ فرکانسی در متلب خواهیم داشت:

این عبارات می توانند به بهترین نحو توسط تبدیل فوریه سریع ارزیابی شوند. یک الگوریتم بسیار کار آمد برای ارزیابی تبدیل فوریه ی گسسته می باشد. این روش مخصوصا برای زمانیکه تعداد داده های نمونه به صورت توانی از ۲ می باشد کار آمد تر خواهد بود نرم افزار متلب الگوریتم توابع گسسته را توسط تابع fft نمایش می دهد.

متلب معکوس گسسته تابع را توسط تابع Ifft نمایش می دهد.

توابع وزنی

موقعیت های گونگونی وجود دارد که وزن دادن به تابع g(t) توسط یک تابع مناسب , جهت ایجاد دقت بیشتر و سایر خواص , در حوزه ی تبدیل فرکانسی مطلوب می باشد. روند کار به این صورت است که سیگنال مرجع , قبل از اجرای تبدیل فوریه ی گسسته اصلاح می شود. در چنین روشی تاثیر تغییرات ایجاد شده با باز کردن تابع , روی مقدار متوسط سیگنال و توان متوسط سیگنال , از بین خواهد رفت . بنابراین اگر مقادیر تعیین شده برای تابع وزنی برابر مقدار زیر باشد در این صورت سیگنال تصحیح شده به صورت رابطه زیر در می آید:

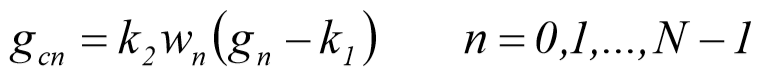
که در آن

و مقدار متوسط تابع

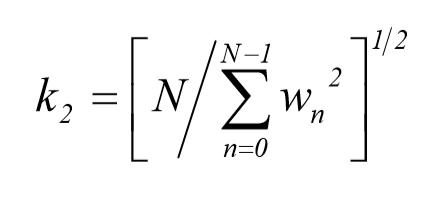
مقدار متوسط توان تابع را تصحیح می کند. سپس کاربر می تواند تبدیل فوریه ی گسسته gcn را محاسبه نماید.

جعبه ابزار پردازش سیگنال دیجیتال متلب شامل هشت تابع وزنی متداول می باشد.

همبستگی عرضی در متلب (Cross Correlation) همبستگی عرضی دو سیگنال قابل محاسبه x(t) و y(t) با زمان محدود توسط رابطه زیر محاسبه می شود

اکنون می خواهیم به عنوان تمرین مقدار این عبارت را با استفاده از تبدیل فوریه ی معکوس تابع چگالی Sxy(W) محاسبه نماییم بنابراین داریم:

که در رابطه فوق F^-1 مبین تبدیل فوریه معکوس می باشد

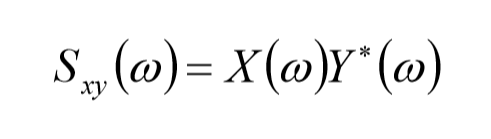
که در آن مقادیر x(w) و y(w) تبدیلات فوریه توابع x(t) و y(t) می باشند و علامت ستاره مبین مزدوج مختلط می باشد. جهت تبدیل Rxy(t) به واحد ای مناسبش باید Sxy(W) را در Δt=T/N ضرب کنیم

تبدیل فوریه موج سینوسی در متلب

فرض نمایید:

باشد بنابراین

وچون

می باشد. فرض می کنیم که تابع g(t) توسط تابع همینگ مطابق زیر وزن دهی شده است:

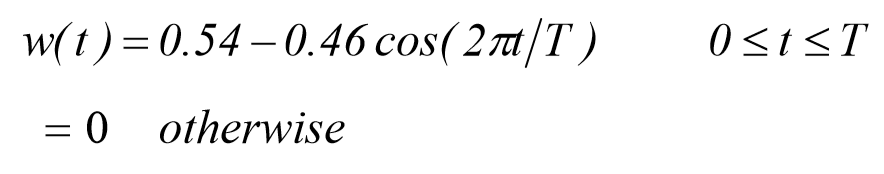
برنامه و جهت محاسبه و رسم سیگنال وزن دهی اصلاح شده gc(t) و دامنه An و همچنین نمایش توان متوسط سیگنال که به صورت زیر می باشد

فرض نمایید داده های اولیه زیر را داریم آنگاه کد نویسی در متلب به صورت زیر می باشد:

با اجرای کد فوق دو شکل زیر در متلب نمایش داده می شوند و پیغام متوسط توان نیز در پنجره فرمان نمایش داده می شود:

توجه نمایید که دامنه موج سینوسی مساوی ۲٫۵ نمیباشد اما این مقدار را می توان با حذف تابع وزنی در پروژه متلب محاسبه نمود.

 

در اینجا آشنایی با محیط متلب بخش هفتاد و سوم به پایان رسیده است و در آموزش های بعدی به مباحث دیگر آموزش متلب می پردازیم. همچنین از شما مخاطبین عزیز سایت همیارپروژه دعوت می کنم که برای انجام پروژه متلب خود آموزش های ما را دنبال نمایید.

 

نویسنده: زهرا رستمی