آشنایی با محیط Matlab

در ادامه آموزش های سایت همیارپروژه برنامه نویسی متلب ارائه خواهد شد .آموزشها از مقدماتی تا پیشرفته ادامه دارد و ما به شما کدنویسی در نرم افزار متلب را یاد خواهیم داد. با ما همراه باشید.

جا بجایی آزاد در طول یک صفحه عمودی گرم در نرم افزار متلب

معادلات توصیف کننده ی جا بجایی آزاد در طول یک صفحه ی عمودی گرم در نرم افزار متلب , که با یک سیال سردتر در تماس است توسط روابط زیر داده می شود.

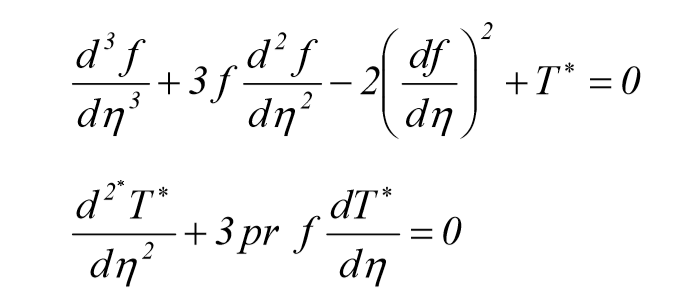
که در معادلات فوق pr=0.7 و شرایط مرزی در ᶋ=۰ به صورت زیر می باشد:

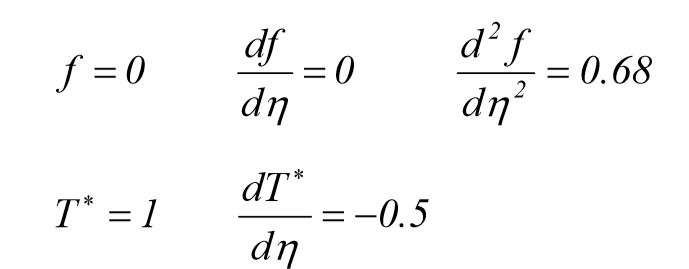
این دستگاه را می توان توسط معرفی مجموعه متغیر های وابسته ی زیر به دستگاهی شامل پنج معادله ی دیفرانسیل مرتبه اول در نرم افزار متلب تبدیل نمود

که در آن y1 تابع جریان, y2 مبین سرعت , y3 مبین برش, y4 نشان دهنده ی در جه حرارت و y5 شدت گرما می باشد. در این صورت معادلات دیفرانسیل بر حسب متغیر های جدید به صورت زیر می باشند:

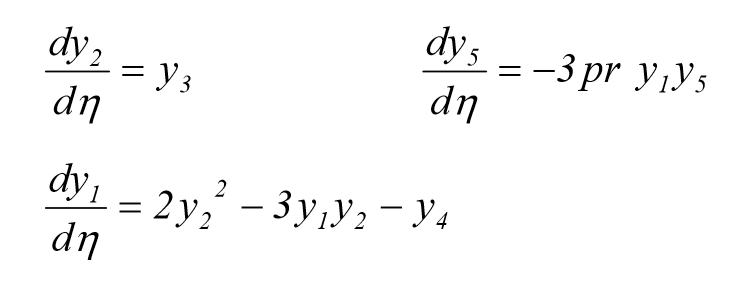
که شرایط مرزی متناظر در ᶋ=۰  به صورت زیر خواهد بود

جهت حل این دستگاه معادلات ابتدا باید تابع زیر را جهت نعیین بردار ستونی نشان دهنده ی طرف راست تساوی های پنج معادله ی فوق , یعنی fi ها تشکیل دهیم.

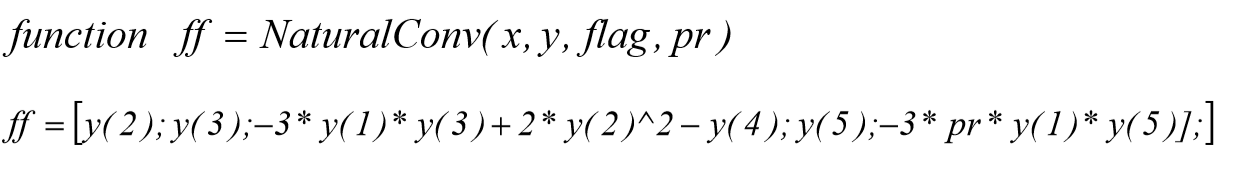
که برنامه ی آن در نرم افزار متلب به صورت زیر می باشد:

 

آونگ معکوس در نرم افزار متلب

پاندول معکوس متصل شده به یک دیسک را در نرم افزار متلب قصد داریم کد نویسی نماییم

معادلات حرکت خطی شده آن به صورت زیر می باشند.

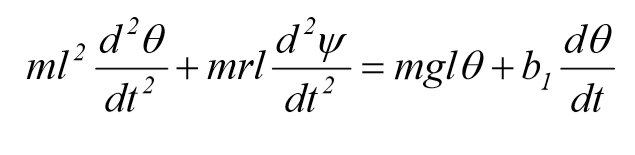
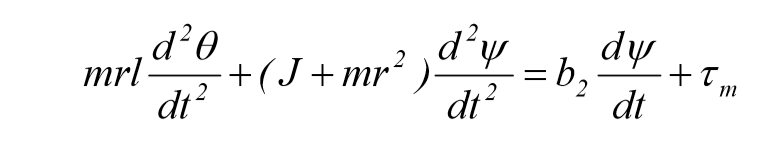
که در آن m جرم وزنه , L طول پاندول و r شعاع دیسک که شامل وزنه ی متصل نیز می باشد, d ضخامت دیسک و اینرسی دیسک به صورت زیر تعریف می شود:

و b1 ضریب اصطکاک اتصال مفصلی در پاندول, b2 ضریب اصطکاک اتصال مفصلی در دیسک, Ꞇm گشتاور اعمال شده توسط موتور متصل به پایه ی دیسک می باشد. اگر مجموعه متغیر های وابسته زیر را تعریف نماییم:

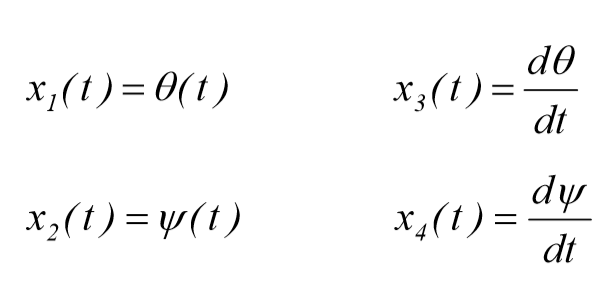
در این صورت معادلات حاکم بر سیستم به فرم ماتریسی در نرم افزار متلب به صورت زیر خواهند بود:

که در آن:

جهت بدست آوردن چهار معادله دیفرانسیل معمولی مرتبه اول که توسط تابع ode45  مورد نیاز می باشد , باید این مجموعه معادلات را برای بدست آوردن رابطه زیر حل نماییم:

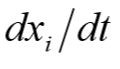
بنابراین

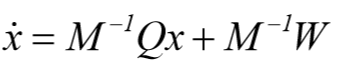
که زمانی عبارت فوق دارای معنی می باشد که دترمینان M مخالف صفر باشد. در این صورت رابطه زیر برقرار است:

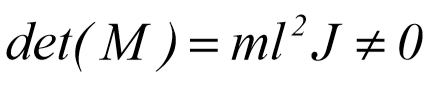
ابتدا تابع زیر را جهت تعیین طرف راست چهار معادله ی دیفرانسیل معمولی مرتبه اول مطابق زیر ایجاد می نماییم

که در آن , برداری ستونی می باشد و کاربر بایستی از تابع InvPend در متلب جهت یافتن پاسخ سیستم در برابر گشتاورهای ناگهانی وارد بر مکانیزم و یا مجموعه ای متشکل از شرایط اولیه , استفاده کند. متاسفانه این سیستم ناپایدار می باشد و حل تحلیلی این مساله منجر به اطلاعات مفیدی نخواهد شد. به علاوه این حل به سرعت منطقه ای که در آن فرضهای خطی سازی معادلات معتبر می باشند, را ترک خواهد کرد. به هر حال, این سیستم را می توان با استفاده از یک کنترلر مناسب پایدار نمود.

شرایط مرزی تعیین شده در دو انتهای بازه ی عمل در نرم افزار متلب

معادله ی دیفرانسیل معمولی زیر را در نظر بگیرید

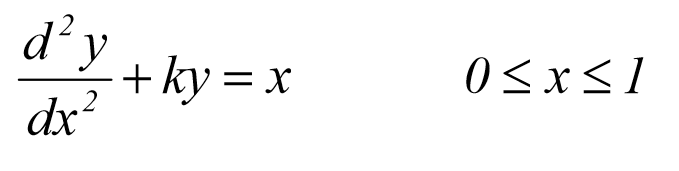
که دارای شرایط مرزی زیر می باشد

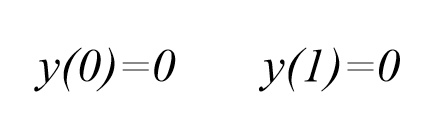
از انجا که تابع ode45 , تنها نیازمند تعیین شرایط مرزی در x=0 می باشد, باید از شرایط زیر برای محاسبه استفاده نماییم

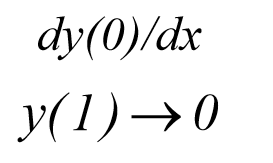
این یک فرآیند تکراری می باشد نا جایی که مقدار y به اندازه کافی به صفر نزدیک شود.

از آنجایی که تنها دارای یک مجهول می باشیم , برای یافتن این مقدار می توانیم از توابع fzero استفاده نماییم. برای معادلات دیفرانسیل مرتبه های بالاتر از دستور fsolve به جای fzero در پروژه های نرم افزار متلب استفاده می نماییم.

در ابتدای طراحی پروژه متلب معادله را به یک جفت معادله دیفرانسیل مرتبه اول تبدیل می نماییم در این صورت دو معادله به صورت زیر خواهد بود.

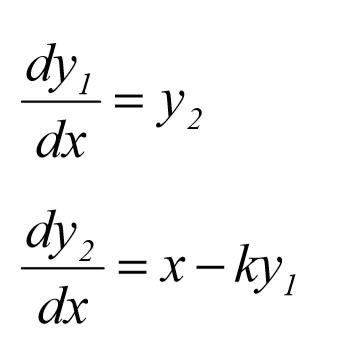
تابع نشان دهنده ی این معادله در قالبی که توسط دستورOde 45 مورد نیاز می باشد. به صورت زیر در متلب نوشته می شود

سپس تابعی را جهت استفاده تابع fzero , برای یافتن مقدار زیر ایجاد می نماییم

که در شرایط زیر برقرار می باشد

توجه نمایید که تابع fzero در متلب مقدار s را آنقدر تغییر می دهد تا z به سمت صفر میل نماید.

 

در اینجا آشنایی با محیط متلب بخش هفتاد به پایان رسیده است و در آموزش های بعدی به مباحث دیگر آموزش متلب می پردازیم. همچنین از شما مخاطبین عزیز سایت همیارپروژه دعوت می کنم که برای انجام پروژه متلب خود آموزش های ما را دنبال نمایید.

 

نویسنده: زهرا رستمی