آشنایی با محیط Matlab

در ادامه آموزش های سایت همیارپروژه برنامه نویسی متلب ارائه خواهد شد .آموزشها از مقدماتی تا پیشرفته ادامه دارد و ما به شما کدنویسی در نرم افزار متلب را یاد خواهیم داد. با ما همراه باشید.

مینیمم محلی یک تابع – تابع fminbnd

تابع fminbnd که متعلق به جعبه ابزار بهینه سازی می باشد , مینیمم محلی تابع F(x) را در بازه a<x<b با تلرانس t0 می یابد. این تابع همچنین می تواند پارامتر های pj را به تابع تعریف کننده ی f(x) انتقال دهد. شکل کلی دستور fminbnd در نرم افزار متلب به صورت زیر می باشد.

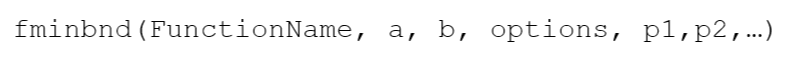
که در آن function name نام فایل تابع در میان علامت کوتیشن بدون پسوند “.m” و یا هنگامیکه توسط دستور inline ساخته شود, نام متغیر تابع بدون استفاده از کوتیشن می باشد B=b , σ=a و متغیر options یک بردار اختیاری که پارامترهایش توسط دستور optimset تعیین می شوند, می باشد. p1 ,p2 و… پارامترهای pj می باشند.

اولین خط غیر دستوری این تابع به شکل زیر می باشد:

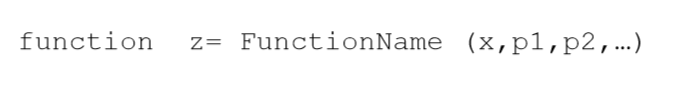
که در آن x متغیر مستقلی است که توسط  تابع fminbnd در متلب جهت یافتن مینیمم f(x) تغییر می کند. متغیر مستقل باید همواره در این موقعیت ظاهر شود. اکنون چگونگی استفاده از دستور fminbnd را شرح می دهیم.

تابع humps را که توسط نرم افزار متلب در شکل زیر نشام میدهد در نظر بگیرید برای یافتن مقدار مینیمم تابع در بازه ی ۰<X<1 از برنامه ی زیر استفاده می کنیم:

که پس از اجرا , خروجی آن به صورت زیر می باشد:

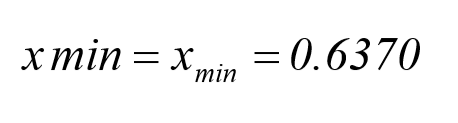
از طرفی اگر بخواهیم مقدار ماکزیمم تابع humps را در این بازه بیابیم, باید تشخیص دهیم که تابع fminbnd را روی مقدار منفی و یا معکوس تابع humps اثر دهیم. بنابراین با استفاده از منفی مقدار تابع humps فایل زیر را می سازیم

که مقدار w=0.300376  را پس از اجرا نمودن ارائه می نماید. مقدار تابع humps در مکان این ماکزیمم توسط دستور زیر به دست می آید.

که نتیجه Wmax=96.5014 را ارائه می کند.

حل عددی معادلات دیفرانسیل معمولی – تابع Ode45

تابع Ode45 یک سیستم شامل n معادله ی دیفرانسیلی معمولی مرتبه اول

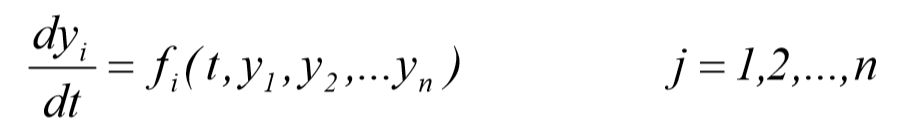
را مطابق زیر در بازه ی t0<T<tf با شرایط اولیه ی زیر حل می نماید.

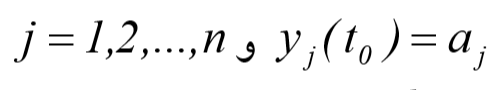
که در ن aj ها مقادیر ثابتی می باشند . آرگومانهای تابع Ode 45 به صورت زیر می باشد.

که در آن خروجی t یک بردار ستونی می باشد که توسط تابع ode45 تعریف می شود. خروجی y ماتریس جوابها می باشد که تعداد سطر های آن متناظر با مرتبه t و تعداد ستونهایش مناظر با حل های زیر می باشد:

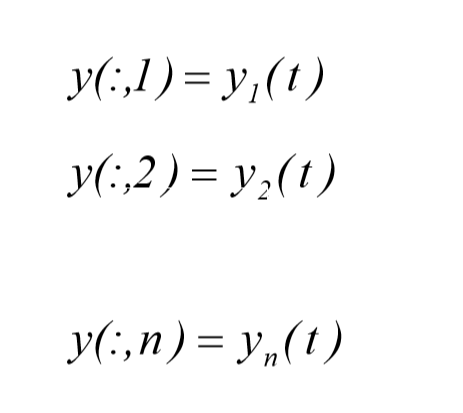
اولین آرگومان تابع ode45 , Function name می باشد, که نام فایل تابع در میان علامت کوتیشن بدون پسوند “.m”  و یا زمانیکه توسط دستور inline ساخته شود , نام متغیر بدون نیاز به استفاده از علامت کوتیشن خواهد بود. به شکل کلی دستور به صورت شکل زیر می باشد:

که در آن متغیر مستقل y برداری است که عناصرش متناظر با yj می باشند, flag یک رشته متشکل از حروف کوچک می باشد و p1,p2 و…  پارامترهای نسبت داده شده به Function name می باشند و yprime یک بردار ستونی با طول n که عناصرش به صورت زیر می باشند:

متغیر های yprime , Function name و … توسط کاربر نسبت داده می شوند. آرگومان دوم ode45 یک بردار دو عنصری که شامل زمان شروع و پایان جهت انجام حل عددی است, می باشد. این کمیت می تواند برداری شامل زمانهای زیر باشد:

که در آنها حل صورت می پذیرد, باشد. آرگومان سوم برداری شامل شرایط اولیه ی زیر می باشد:

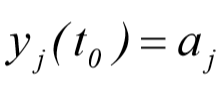
آرگومان چهارم, options معمولا تهی می باشد

سایر آرگومانها به تابع Function Name انتقال داده خواهند شد.

چهار حل کننده ی معادلات دیفرانسیل معمولی دیگر در نرم افزار متلب وجود دارد که هر یک از آنها دارای مزایای خاص خود, بسته به ویژگی ها و شرایط مربوطه می باشند. که این چهار تابع ode 23 , ode113 , ode15s , ode23s می باشند. نحوه ی استفاده نمودن از این توابع همانند تابع ode 45 می باشد.

نحوه استفاده از این تابع را با در نظر گرفتن معادله ی دیفرانسیل معمولی مرتبه دوم زیر توضیح می دهیم:

این معادله را می توانیم با احتساب تغییر متغیر های زیر به صورت دستگاهی متشکل از دو معادله ی دیفرانسیلی معمولی مرتبه اول در نظر گرفت

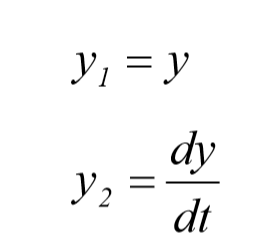
در این صورت داریم:

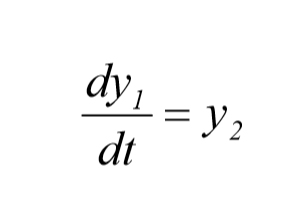
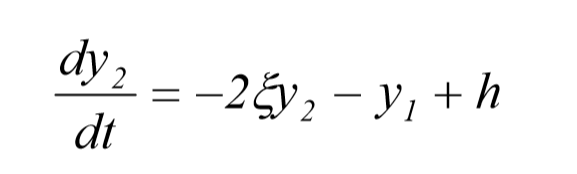
اجازه دهید سه مورد زیر که در همه ی آنها مقادیر زیر ثابت اند را در نظر بگیریم:

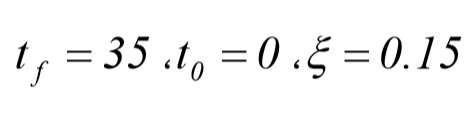
مورد اول

که U(t) مبین تابع پله ای اول می باشد

مورد دوم

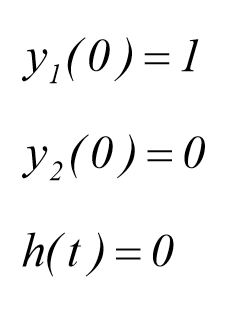
مورد سوم

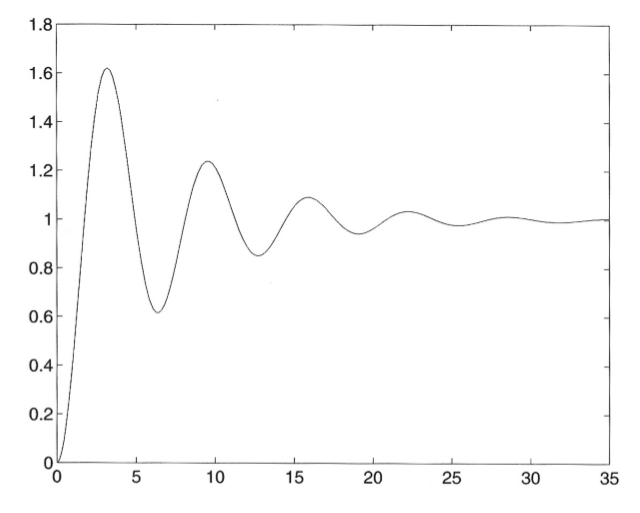
در ابتدا تابعی به جهت اداره ی این سه مورد می سازیم و خروجی را به شکلی که توسط دستور ode45 مورد نیاز می باشد نشان خواهیم دادم

 

در اینجا آشنایی با محیط متلب بخش شصت و نهم به پایان رسیده است و در آموزش های بعدی به مباحث دیگر آموزش متلب می پردازیم. همچنین از شما مخاطبین عزیز سایت همیارپروژه دعوت می کنم که برای انجام پروژه متلب خود آموزش های ما را دنبال نمایید.

 

نویسنده: زهرا رستمی