آشنایی با متلب ( نکات کاربردی-۱۴)جمعه 03, جولای 2020

آشنایی با محیط Matlab
در ادامه آموزش های سایت همیارپروژه برنامه نویسی متلب ارائه خواهد شد .آموزشها از مقدماتی تا پیشرفته ادامه دارد و ما به شما کدنویسی در نرم افزار متلب را یاد خواهیم داد. با ما همراه باشید.
حل معادلات خطی
روش ماتریس
بسیاری از معادلات خطی قابل نمایش به فرم ماتریسهای ساده می باشند و می توان با قوانین مربوط به ماتریسها به راحتی اقدام به حل اینگونه معادلات نمود. برای مثال دستگاه زیر را در نظر بگیرید

دستگاه فوق را می توان به فرم زیر نوشت

برای حل اینگونه معادلات هیچ محدودیتی وجود ندارند البته در حالت کلی اگر دترمینان ماتریس A صفر گردد دستگاه جواب نخواهد داشت. به مثال زیر توجه نمایید:

حل دستگاه چند معادله و چند مجهول با دستور Solve
دستور solve در متلب برای حل معادلات به کار برده می شود.اگر بخواهیم یک دستگاه چند معادله و چند مجهول را حل نماییم باید معادلات را به دستور Solve بدهیم تا این دستور , پاسخ دستگاه را محاسبه نماید .به مثال زیر توجه نمایید
فرض نمایید بخواهیم دستگاه دو معادله و دو مجهول را که به صورت زیر می باشد حل نمایید. برای این منظور باید دو معادله را درون پرانتز دستور Solve بنویسیم . و هر معادله باید درون دو علامت ‘ قرار بگیرد


دستور

دستگاه دو معادله و دو مجهول را حل می نماید و عبارت

نیز برای نمایش نتایج به دست می آید

مثال
فرض نمایید قصد داریم دستگاه سه معادله و سه مجهول زیر را حل نماییم:
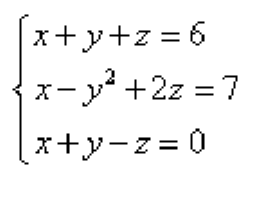
خواهیم داشت:

با حل معادله خواهیم داشت:

مشتق گیری از عبارت های سمبلیک با دستور diff
عموما در علم ریاضی بسیار خواهید دید که بخواهید مشتق یک عبارت را محاسبه نمایید. در نرم افزار متلب برای آنکه بتوانیم عبارتی مشتق بگیریم نخست باید متغیرهای به کار رفته در آن عبارت را با استفاده از دستور Syms به صورت سمبلیک تعریف نماییم. سپس با دستور diff می توانیم مشتق آن عبارت را محاسبه نماییم.
به مثال زیر توجه نمایید:
قصد داریم مشتق عبارت زیر را محاسبه نماییم
![]()
نتیجه خواهد بود:

همانطور که میبینید مشتق عبارت در خروجی نمایش داده شد . دستور Syms x سبب می شود که در نرم افزار متلب , متغیر x به صورت سمبلیک تعریف گردد.
نکته:
می توانیم ابتدا با استفاده از دستور inline تابعی را به صورت f(x) تعریف نماییم و سپس از این تابع بر حسب متغییر x مشتق بگیریم. به مثال زیر توجه نمایید.

و می توانیم نتیجه را به صورت زیر مشاهده نماییم.

مشتق مرتبه دوم و مرتبه های بالاتر با دستور diff
برای گرفتن مشتق مرتبه دوم و یا مرتبه های بالاتر باید در دستور diff مرتبه مشتق را مشخص کنیم. به مثال زیر دقت نمایید
مثال:

نتیجه به صورت زیر خواهد بود:

مشاهده می کنید که مشتق مرتبه دوم عبارت x4 در خروجی نمایش داده شده است. مرتبه دوم بودن مشتق را با نوشتن عدد ۲ در درون پرانتز دستور diff مشخص کرده ایم.
نکته:
اگر بخواهیم از عبارت x4 مشتق مرتبه n ام بگیریم باید دستور را به صورت زیر اجرا نماییم.

حل معادله دیفرانسیلی در متلب با دستور dsolve
این دستور برای حل معادلات دیفرانسیلی در نرم افزار متلب به کار می رود. فرض نمایید تابعی مانند y تابعی از متغیر x باشد. معادله دیفرانسیلی شامل مشتق مرتبه اول و یا مرتبه های بالاتر از y خواهد بود. اما چگونه باید y’ را برای دستور dsolve مشخص می کنیم. روش مورد استفاه این است که به جای y’ از نماد D استفاده می نماییم.مثال زیر را در نظر بگیرید
معادله دیفرانسیل زیر را در نظر بگیرید وآنرا حل نمایید.
![]()
![]()
نتیجه:

مشاهده می کنید که پاسخ معادله دیفرانسیلی در خروجی نمایش داده شده است
حل معادلات با شرایط مرزی
کافی است شرایط مرزی را در تابع dsolve وارد نماییم
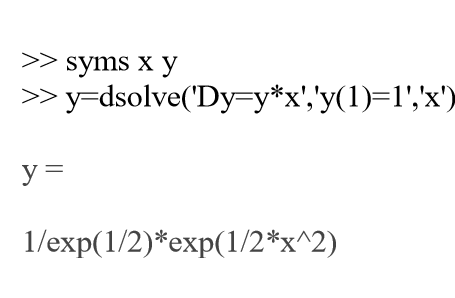
به مثال دیگری توجه نمایید:


بعد از حل معادله, برای نمایش بهتر y , می توان دستور pretty را اجرا نمود.
حل معادلات دیفرانسیل مرتبه دوم و بالاتر
همانطور که گفتیم مشتق مرتبه اول y’ را با نماد Dy برای دستور dsolve مشخص می کنیم. اما گار مشتق مرتبه دوم و یا بالاتر باشد آنگاه باید ابتدا نماد D را نوشته , سپس عدد مربوط به مرتبه مشتق را بنویسیم و در آخر نیز نماد y نوشته شود. مثلا برای تعریف y’’ باید نماد D2y و برای تعریف y’’’ باید نماد D3y را به کار ببریم.
معادلات مرتبه دوم
در این صورت نیز همانند معادلات مرتبه اول از تابع dsolve استفاده می کنیم. به عنوان نمونه , معادله زیر را به کمک Matlab حل می نماییم.
![]()

دستگاه معادلات دیفرانسیل خطی
در این حالت باز هم از دستور dsolve استفاده می شود. با این تفاوت که تمامی معادلات را وارد دستور می نماییم.


مثالی دیگر


انتگرال گیری در متلب با دستور int
معمولا دستورات انتگرال گیری به دو شیوه صورت می پذیرد. در شیوه نخست, حدود بالا و پایین انتگرال مشخص نیست اما تنها به صورت سمبلیک انتگرال را محاسبه می کنیم. در شیوه دوم حدود بالاو پایین انتگرال مشخص می باشد و با توجه به حد بالا و پایین, مقدار انتگرال محاسبه می شود و نتیجه به صورت عدد در خروجی نمایش داده می شود, در متلب دستور int به هر دو شیوه ذکر شده می تواند انتگرال را محاسبه نماید.
انتگرال نامعین
زمانی که حد بالا و پایین انتگرال مشخص نباشه باید تنها عبارت زیر انتگرال و همچنین متغیری که باید بر حسب آن انتگرال گرفته می شود را برای دستور int مشخص کنیم به مثال زیر دقت کنید:
فرض کنید بخواهیم انتگرال زیر را محاسبه نماییم:

بنابراین خواهیم داشت:
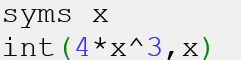
در نتیجه, حاصل به صورت زیر خواهد بود:

در اینجا آشنایی با محیط متلب بخش شصت و یکم به پایان رسیده است و در آموزش های بعدی به مباحث دیگر آموزش متلب می پردازیم. همچنین از شما مخاطبین عزیز سایت همیارپروژه دعوت می کنم که برای انجام پروژه متلب خود آموزش های ما را دنبال نمایید.
نویسنده: زهرا رستمی










دیدگاهتان را بنویسید