شبکه SVM در متلب

در ادامه آموزش های سایت همیارپروژه برنامه نویسی متلب ارائه خواهد شد .آموزشها از مقدماتی تا پیشرفته ادامه دارد و ما به شما کدنویسی در نرم افزار متلب را رایگان یاد خواهیم داد. با ما همراه باشید.

شبکه SVM در متلب

نوع خاصی از شبکه های SVM ماشین بردار پشتیبان یا عصبی هستند که بر خلاف سایر انواع شبکه های عصبی ( مانند به جای کمینه کردن خطا, ادام به کمینه RBF ) و MLP کردن ریسک عملیاتی طبقه بندی یا مدل سازی می کند. این ابزار , بسیار قدرتمند است و در زمینه های مختلفی چون طبقه بندی, خوشه بندی و مدل سلزی ( رگرسیون) می توان مورد استفاده قرار بگیرد.

شکل زیر با دو نوع داده را در نظر بگیرید.

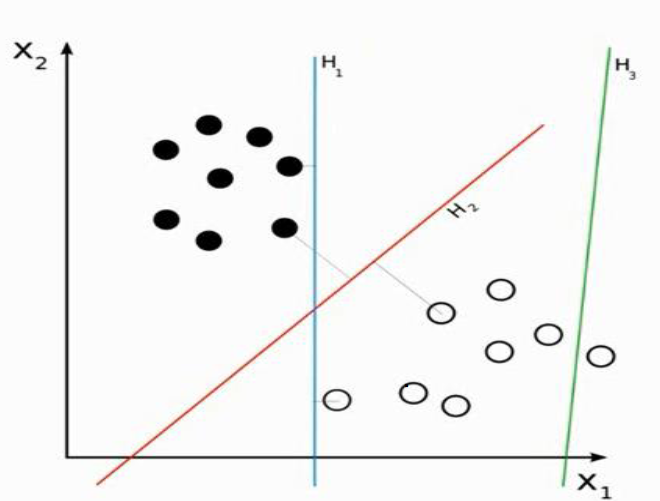
با توجه به شکل اصولا H3 که تفکیک کننده این دو مجموعه نمی باشد در مورد H1 و H2 که هر دو تفکیک کننده هستند و با روش SVM به دنبال بهترین تفکیک کننده مینیمم ریسک عملیاتی هستیم که در ادامه به آن می پردازیم.

توجه داشته باشید که هر گاه با یک شبکه عصبی MLP کار می کردیم هر دو H1 و H2 به یک اندازه می توانند به عنوان جدا کننده عمل کنند ولی در SVM خواهیم دید که H2 تفکیک کننده بهتری می باشد.

SVM خطی

در یک فضای n بعدی معادله با مفهوم Hyperplan به صورت زیر است.

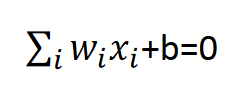
که در حالت دو بعدی خط و در حالت سه بعدی صفحه زیر را خواهیم داشت

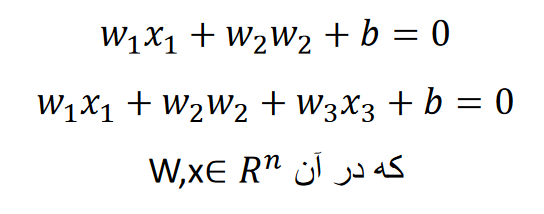
معادله ی تفکیک کننده در حالت کلی به صورت

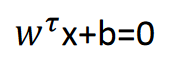
می باشد و به صورت زیر فضای صفحه را به دو قسمت تقسیم می کند.

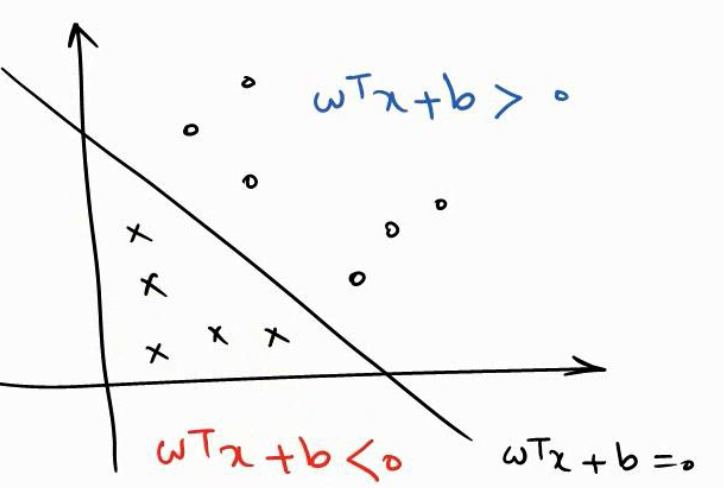
در SVM به جای استفاده از این خط دو خط موازی آن را در نظر می گیریم.

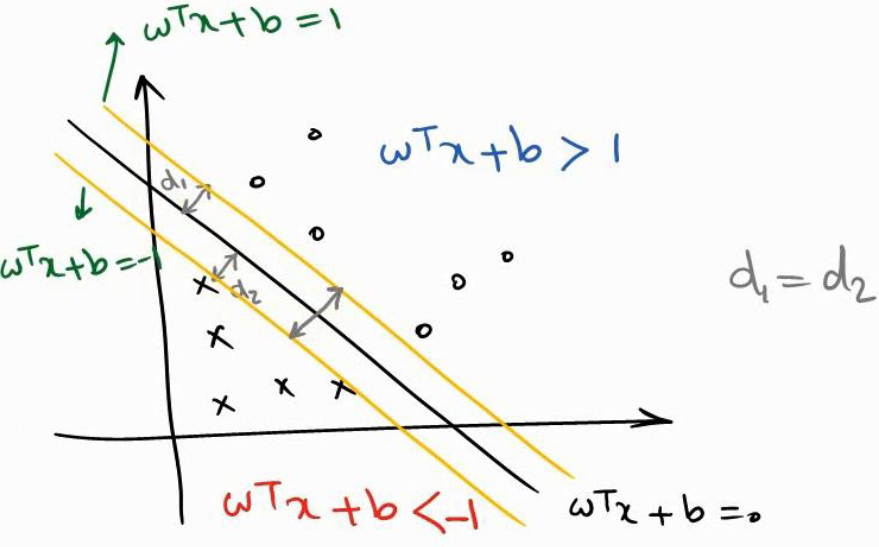
به طوریکه در فاصله بین دو خط اجازه حضور عنصر وجود ندارد.

در واقع بیان این مورد به صورت زیر می باشد. فرض کنید مجموعه ای از n داده داریم:

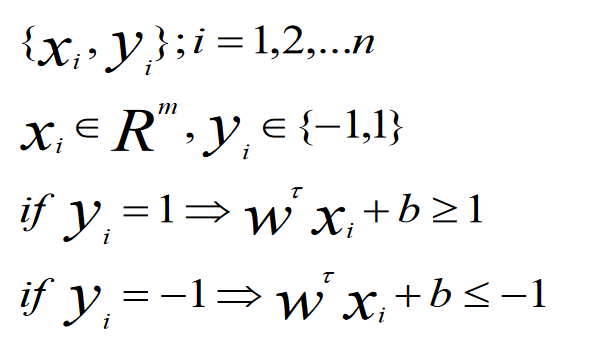
فاصله ایجاد شده مقاومت در برابر ریسک انتخاب تفکیک کننده را افزایش می دهد یعنی تفکیک کننده ای بهتر عمل می کند که فاصله d بیشتری داشته باشد. حال می خواهیم این فاصله d را محاسبه نماییم.

شکل زیر را در نظر بگیرید . w بردار نرمال و میدانیم هر نقطه روی خط L فاصله اش از مبدا مضربی از W خواهد بود.

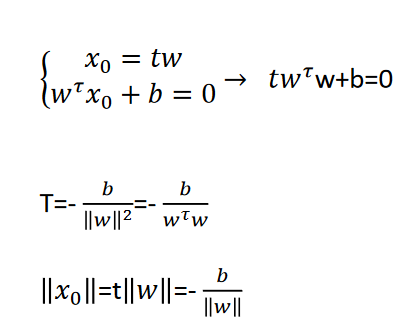
برای حل مساله ضریبی از قیود مساله را به تابع هدف اضافه می کنیم ( شبیه مسائل که اصطلاحا تابع جریمه نام دارد.)

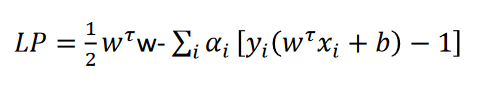
حل مساله LP میبینیم که جواب مساله یک نقطه زنی یا (saddle point) است یعنی باید مساله نسبت به تعدادی از متغیرها مینیمم (b,w) و نسبت به تعدادی دیگر (α) ماکزیمم شود.

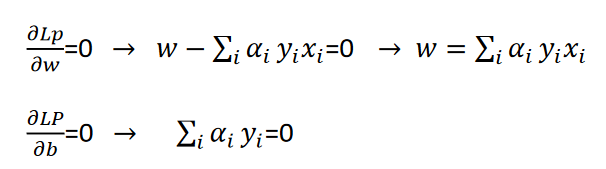
با جایگزاری این مقادیر در مساله LP مساله به صورت LD به صورت زیر به دست می آید.

این یک مساله Quadratic programming یا برنامه ریزی درجه ۲ است که در متلب برنامه quadprog این مساله را حل می کند و جواب α را بدست می آورد.

هر گاه شرایط K.K.T برای بهینه سازی روی این مساله اعمال شود برای جواب بهینه باید شرایط زیر بر قر  ار باشد.

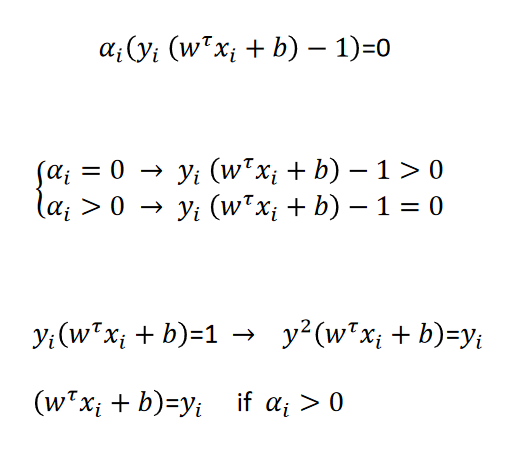
که شکل کلی یک single perseptron می باشد . وزنها و بایاس به نحوی تعیین می شوند که d بیشینه شود و این همان راه حلی است که جواب مساله را به صورت H2 می برد.

آنچه که تا به اینجا گفتیم مربوط به SVM hard margin است و در حالت کلی کاربردی نیست زیرا یک طبقه بندی صرفا خطی است و برای کاربردی کردن SVM soft margin را معرفی می کنیم.

فرض نمایید عنصری از کلاس A در داخل کلاس B باشد یا بر عکس در اینصورت برای بردار پشتیبان آن عنصر یک مقدار جریمه در نظر گرفته می شود.

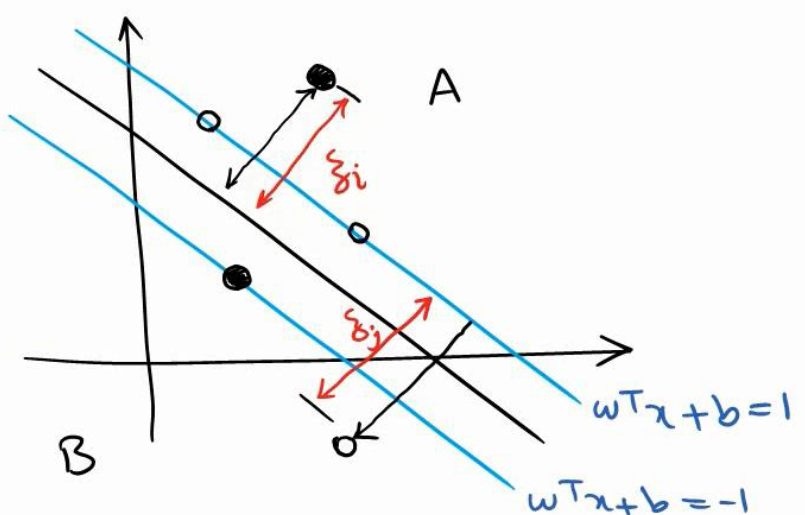
اعضای کلاس A دایره های توخالی و اعضای کلاس B دایره های توپر هستند.

فرض کنید که Ƌ میزان جریمه برای تخطی عضو i ام را نشان می دهد.

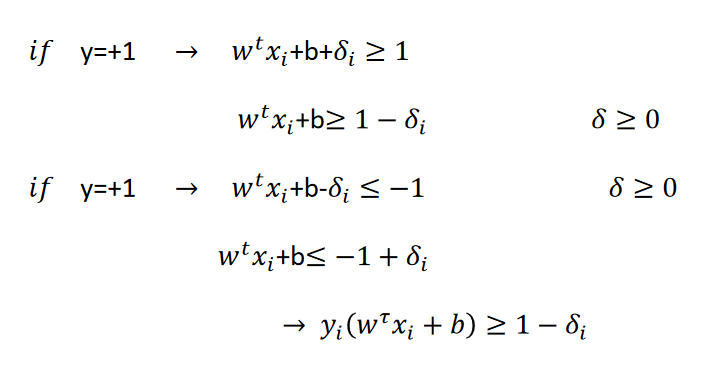
مساله به صورت زیر در می آید.

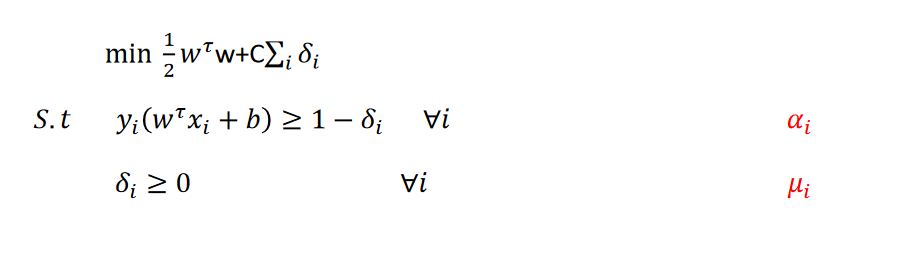
مساله فوق primal problem نام دارد و مولفه هایی که با رنگ قرمز نشان داده شده اند  ضرایب لاگرانژ نام دارد که برای تعریف مساله Doal بکار می رود.

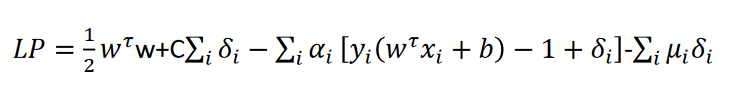
با داشتن سه مولفه زیر داریم:

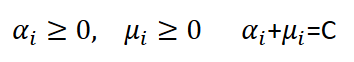
و نتایج زیر را که به صورت Box Constraint معروف هستند را به دست می آوریم.

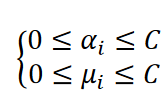
در نهایت بخش Hard margin مساله به صورت زیر به دست می آید.

در واقع Box cons تنها تفاوت بین soft  و hard می باشد و می توان گفت در قسمت hard ضریب c برابر بی نهایت است.

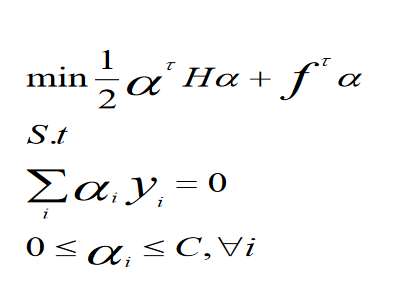
این یک مساله Quadratic programming یا برنامه ریزی درجه ۲ است که در متلب برنامه quadprog این مساله را حل می کند و جواب α به صورت زیر محاسبه می شود.

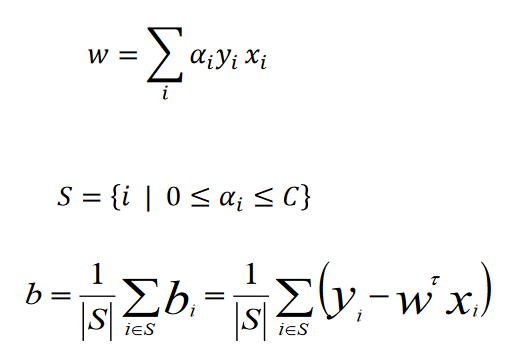
به صورت عملی soft margin را در نرم افزار متلب پیاده سازی خواهیم کرد و میزان C در عمل به صورت آزمون و خطا تعیین می شود. البته می توان برای تعیین مقدار بهینه C از الگوریتم های بهینه سازی GA یا PSO یا ICA و.. می توان استفاده نمود. در نرم افزار متلب Boxbinformatic یک SVM برای حل حالت باینری درنظر گرفته شده است که کلاسبندی مسائل باینری را می توان انجام داد.

 

در اینجا آشنایی با محیط متلب بخش نود و دوم به پایان رسیده است و در آموزش های بعدی به مباحث دیگر آموزش متلب می پردازیم. همچنین از شما مخاطبین عزیز سایت همیارپروژه دعوت می کنم که برای انجام پروژه متلب خود آموزش های ما را دنبال نمایید.

 

نویسنده: زهرا رستمی

جهت سفارش پروژه به لینک زیر مراجعه نمایید :

سفارش پروژه

همچنین می توانید برای ارتباط سریعتر با شماره و آیدی تلگرام زیر تماس حاصل کنید :
۰۹۱۲۹۵۴۰۱۲۲ – آیدی تلگرام : @fnalk

از طریق کلیک برروی آیکن های زیر میتوانید پروژه خود را در تلگرام و یا واتساپ برای ما ارسال کنید:

ثبت سفارش در واتس آپ ثبت سفارش در تلگرام