بسط به كسرهاي جزيي يا فرم باقيمانده  در متلب

در ادامه آموزش های سایت همیارپروژه آموزش نرم افزار متلب ارائه خواهد شد .آموزشها از مقدماتی تا پیشرفته ادامه دارد و ما به شما نرم افزار را یاد خواهیم داد. با ما همراه باشید.

بسط به كسرهاي جزيي يا فرم باقيمانده  در متلب(Residue Form)        

هر تابعي تبديلي به فرم باقيمانده به شكل زير قابل نمايش است :

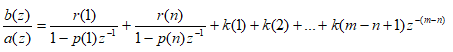
با تابع  residuez به تبديل تابع تبديل به حالت بسط كسرهاي جزيي هستند .

residuez در خروجي در يك بردار ستوني p مكان قطب ها ، در يك بردار ستوني ديگر r باقيمانده هاي مربوط به همان قطب ها و در يك بردار سطري k نيز ساير بخش ها را مي دهد .

اگر تفاضل ۲ قطب كمتر از ۰٫۰۱ دامنه هر كدام باشد ، residuez آن ها را يكسان فرض مي كند .

براي مثال فرم باقيمانده  برابر است با :

كه معادل با است براي يافتن معكوس تبديل z اين عبارت ، بايد معكوس تبديل z هركدام از دو جمله آن را محاسبه كرد كه  را مي دهد .

براي انجام اين محاسبه در خط دستورات به شكل زير عمل مي شود :

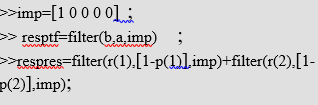
مدل سيستم هاي پيوسته در زمان در متلب:

اين مدل ها نشان دهنده سيستم ها فيلترهاي آنالوگ هستند.

بسياري از مدل هاي گفته شده در بالا براي سيستم هاي گسسته مانند مدل صفر و قطب .

تابع تبديل و بسط به توابع جزيي براي نمايش سيستم هاي پيوسته نيز به كار مي روند .

براي تبديل بين روش هاي مختلف مدل سيستم خطي مي توان از  دستورات ارائه شده در جدول ۱-۱ استفاده كرد .

ستون اول نشان دهنده مدل مبدأ و سطر اول نشان دهنده مدل هاي مقصد است .

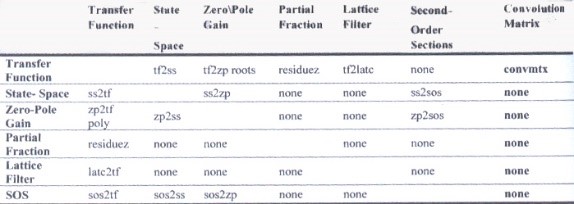
توجه شود كه تبديل از يك ساختار فيلتر به مدل هاي ديگر ممكن است .

نتايج متفاوتي داشته باشد كه دليل اين امر دقت محدود رياضي كامپيوتر و تغييرات در زمان گرد كردن اعداد است .

تبديل فوريه گسسته در متلب

تبديل فوريه گسسته يا DFT يكي از ابزراهاي اساسي در پردازش سيگنال هاي ديجيتال است.

اساس جعبه ابزار  پردازش سيگنال تبديل فوريه سريع FFT كه همان DFT است كه زمان اجراي آن كاهش يافته است .

توابع fft و ifft براي محاسبه تبديل فوريه گسسته و معكوس آن استفاده مي شود .

فرض كه داده ورودي به x,fft باشد، در خروجي تبديل يافته آن ، y است كه با آن هم طول بوده و تبديل فوريه گسسته آن  در فركانس هاي هم فاصله حول دايره واحد مي باشد .

براي مثال يك بردار سيگنال زمان به شكل زير را در نظر بگيريد :

تبديل DFT سيگنال و دامنه و فاز دنباله خروجي آن به شكل زير هستند :

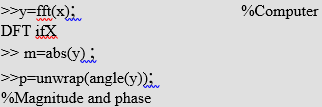
براي رسم دامنه و فاز از دستورات زير استفاده مي شود :

دومين پارامتر ورودي تابعfft معرف تعداد نقاطي است كه DFT در آن ها نشان داده مي شود .

اگر n  از تعداد نقاط دنباله ورودي بيشتر باشد ، fft عمل  zero padding را انجام مي دهد و اگر كمتر باشد تعدادي از نقاط حذف مي شوند.

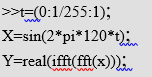
طراحي و پياده سازي فيلتر در متلب

طراحي فيلتر  به معني ساخت ضرايب است به نحوي كه بعضي از ملزومات فيلتركردن را برآورده كند .

پياده سازي فيلتر  به معني انتخاب و به كار بردن يك ساختار فيلتر  خاص روي اين ضرايب است .

تنها پس از طراحي و پياده سازي فيلتر  است كه مي توانيد داده را فيلتر  كنيد .

دراين بخش طراحي و پياده سازي فيلتر بررسي خواهد شد .

هدف از طراحي فيلتر  ايجاد تغييرات وابسته به فركانس در دنباله داده است .

براي مثال لازم است كه نويز ۳۰Hz را از يك دنباله داده كه با نرخ ۱۰۰Hz نمونه برداري شده حذف كرد كه بيان كننده يك مساله كلي است .

براي فيلتر  مورد نياز بيان شده در بالا ، معمولاً يك فيلتر باتروث مناسب است.

براي طراحي يك فيلتر باتروث درجه ۵ پايين گذربا فركانس قطع ۳۰Hz و اعمال آن  به داده x به شكل زير عمل مي شود :

مولفه دوم در تابعbutter نشان دهنده فركانس قطع است كه به نصف فركانس نمونه برداري نرماليزه شده است .

در اینجا آشنایی با نرم افزار متلب قسمت صد و نهم به پایان می رسد و در آموزش های بعدی به مباحث دیگر نرم افزار متلب می پردازیم. همچنین از شما مخاطبین عزیز سایت همیارپروژه دعوت می کنم که برای انجام پروژه های متلب خود آموزش های ما را دنبال نمایید.

نویسنده : زهرا رستمی

جهت سفارش پروژه به لینک زیر مراجعه نمایید :

سفارش پروژه

همچنین می توانید برای ارتباط سریعتر با شماره و آیدی تلگرام زیر تماس حاصل کنید :
۰۹۱۲۹۵۴۰۱۲۲ – آیدی تلگرام : @fnalk

از طریق کلیک برروی آیکن های زیر میتوانید پروژه خود را در تلگرام و یا واتساپ برای ما ارسال کنید:

ثبت سفارش در واتس آپ ثبت سفارش در تلگرام