آشنایی با محیط Matlab

در ادامه آموزش های سایت همیارپر

وژه برنامه نویسی متلب ارائه خواهد شد .آموزشها از مقدماتی تا پیشرفته ادامه دارد و ما به شما کدنویسی در نرم افزار متلب را یاد خواهیم داد. با ما همراه باشید.

فیلتر باترورث

می توانیم این فیلتر را به صورت مربع دامنه اش به صورت زیر بیان نماییم

Ω_c در آن فرکانس قطع می باشد و N مشخص کننده درجه فیلتر است که در این تابع با رسیدن مقدار دامنه به ۰٫۷ مقدار خود برابر صفر می شود . به این فرکانس , فرکانس نصف قدرت نیز گفته خواهد شد. و این نام گذاری به سبب این است که مربع دامنه نصف مربع دامنه در فرکانس DC می باشد. مقدار شیب افت در باند انتقالی ۲۰Ndb/dec است. N قطب این فیلتر حول نیم دایره ای می باشد که شعاع آن Ω_c است و در سمت چپ محور jΩ قرار می گیرد.

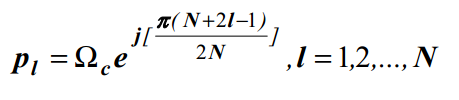
جهت طراحی یک فیلتر باترورث در نرم افزار متلب نیازمند کد نویسی هایی به صورت زیر می باشیم

جهت تعیین درجه فیلتر در کد نویسی خواهیم داشت:

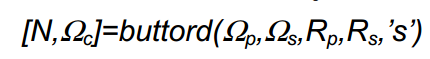
جهت محاسبه ضرایب تبدیل در کد نویسی داریم:

به مثال زیر دقت نمایید:

برای تعیین درجه فیلتر  کد زیر را در نرم افزار متلب می نویسیم:

برای محاسبه ضرایب تابع تبدیل  کد زیر را در نرم افزار خواهیم داشت:

و در نهایت شکل نمودار این فیلتر برابر می شود با:

فیلتر چپی چف۱

مربع دامنه پاسخ فیلتر چپی شف به قرار زیر خواهد بود:

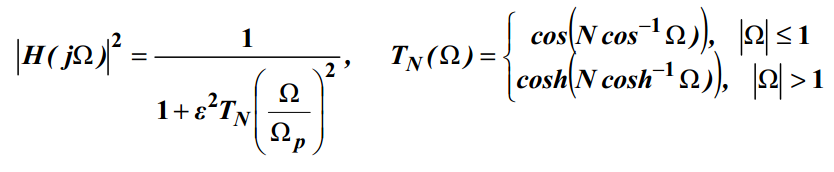
در رابطه ی فوق N درجه فیلتر را تعیین می نماید و Ωp لبه باند گذر و ε مربوط به ریپل باند گذر می باشد. N که قطبهای این فیلتر می باشد در سمت چپ محور jΩ قرار خواهد گرفت

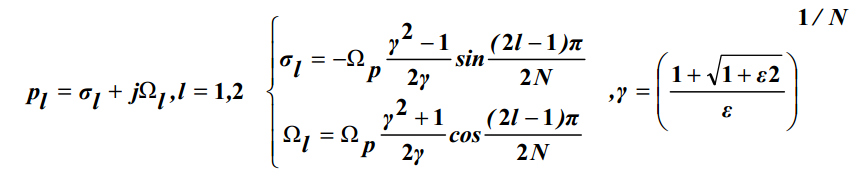
می توانیم این فیلتر را به این صورت نیز تعریف کنیم که یک فیلتر تمام قطب با نوسان در باند گذر می باشد.

برای طراحی این فیلتر در نرم افزار متلب نیازمند کد نویسی تعیین درجه فیلتر هستیم که به صورت زیر خواهد بود:

و سپس برای محاسبه ضرایب تابع تبدیل خواهیم داشت:

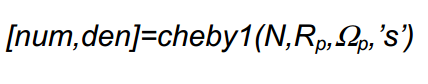
حال به مثال زیر دقت نمایید:

جهت تعیین درجه ی فیلتر داریم:

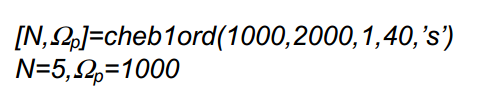
و برای محاسبه ضرایب تابع تبدیل این فیلتر خواهیم داشت:

شکل این تابع به قرار زیر خواهد بود:

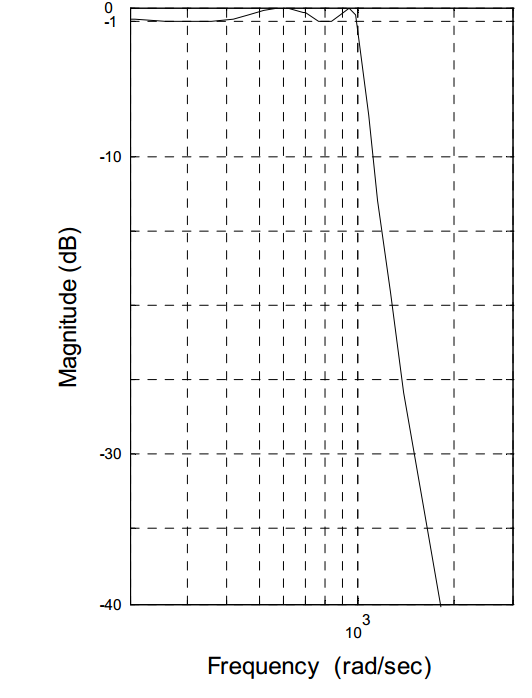
چپی شف نوع ۲

مربع دامنه پاسخ فیلتر چپی شف به صورت زیر خواهد بود:

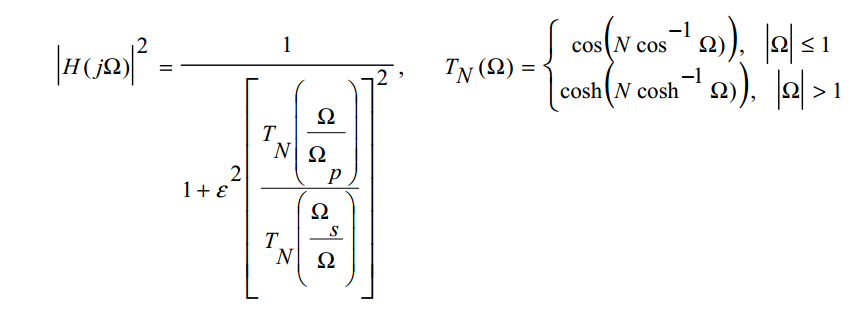
در رابطه فوق N درجه فیلتر می باشد و Ωs لبه ی باند حذف و Ωp لبه ی باند گذر و ε مربوط به ریپل باند گذر خواهد بود. این فیلتر دارای N قطب و صفر می باشد . قطب های این فیلتر عبارتند از:

و صفر های آن به صورت زیر محاسبه خواهند شد:

این فیلتر در باند حذف دارای نوسان می باشد . اگر درجه ی فیلتر زوج باشد در این صورت درجه ی صورت و مخرج بایکدیگر برابر می شود و در این صورت تضعیف نویزهای فرکانس بالا با مشکل روبرو خواهد شد . اما وقتی درجه فرد باشد یکی از صفرها در بی نهایت و درجه صورت یکی کمتر از مخرج می گردد تا تضعیف -۲db/dec در فرکانسهای بالا را تضمین نماید.

کدهای مورد نیاز این فیلتر در نرم افزار متلب به قرار زیر خواهد بود:

برای تعیین درجه فیلتر داریم:

محاسبه ضرایب تابع تبدیل به قرار زیر می باشد:

به مثال زیر دقت نمایید:

جهت تعیین درجه فیلتر خواهیم داشت:

و برای محاسبه ضرایب تبدیل نیر می توان نوشت:

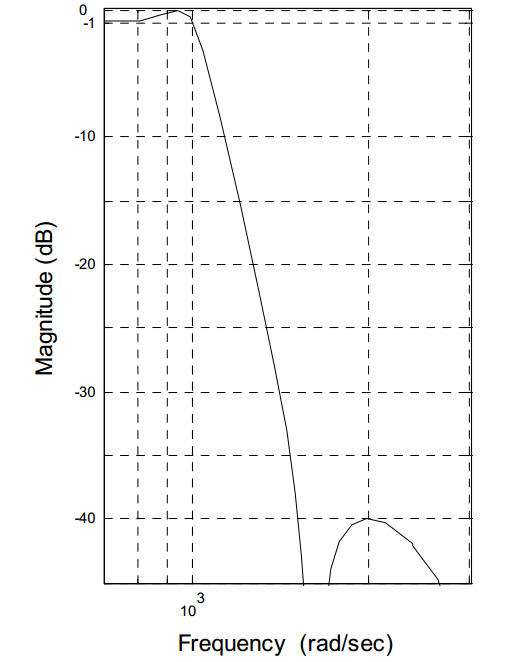
و نمودار خروجی این فیلتر به صورت زیر خواهد بود:

فیلتر Eliptic (cauer filter)

مربع دامنه پاسخ فیلتر الیپتیک به صورت زیر نوشته می شود:

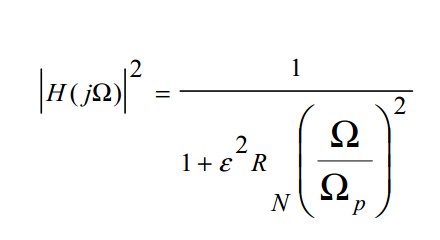
این فیلتر دارای روابط بسیار مفصلی است که در اینجا از بیان آن خودداری می نماییم . اگر در این فیلتر درجه زوج باشد , در این صورت درجه صورت و مخرج کسر برابر می گردد و در نتیجه تضعیف نویزهای فرکانس بالا با مشکل روبرو خواهد شد اما وقتی درجه فیلتر فرد باشد یکی از صفر ها در بی نهایت و درجه صورت یکی کمتر از مخرج خواهد شد تا تضعیف  -۲۰db/dec در فرکانس های بالا را تضمین نماید.

جهت طراحی این فیلتر در نرم افزار متلب داریم:

برای تعیین درجه فیلتر به صورت زیر کد نویسی می کنیم:

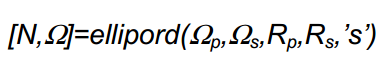
و به جهت محاسبه نمودن ضرایب تابع تبدیل خواهیم داشت:

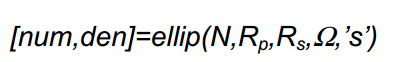
حال به مثال زیر دقت نمایید:

برای تعیین درجه فیلتر داریم:

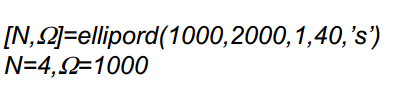
و به جهت محاسبه ضرایب تابع تبدیل فیلتر نیز داریم:

شکل این فیلتر نیز به قرار زیر خواهد بود:

فیلتر بسل linear phase

فیلتر بسل یک فیلتر تمام قطبی می باشد که مشخصه ویژه آن دارا بودن فاز خطی در محدوده باند گذر می باشد و تابع تبدیل این فیلتر به صورت زیر می باشد:

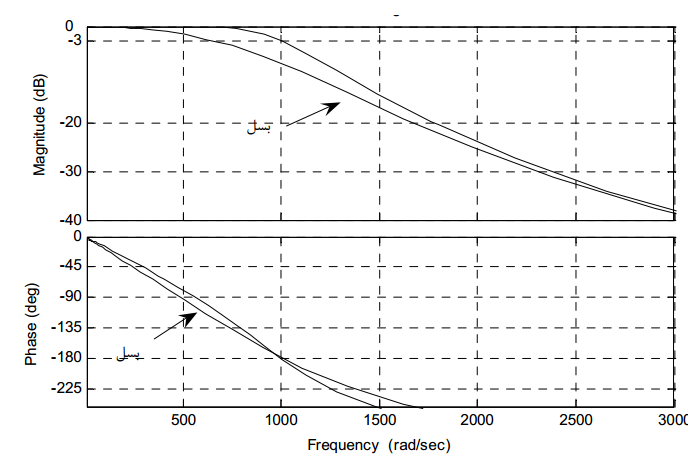
به شکل های زیر توجه نمایید:

همانطور که مشخصس است در این شکل ها به بررسی و مقایسه دامنه و فاز فیلتر باترورث درجه ۴ و بسل درجه ۴ پرداخته شده است . به فاز خطی بسل تا فرکانس ۱۰۰۰ توجه نمایید.

طراحی فیلتر بسل در نرم افزار متلب :

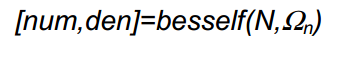
در اینجا آشنایی با محیط متلب بخش بیست و سوم به پایان رسیده است و در آموزش های بعدی به مباحث دیگر آموزش متلب می پردازیم. همچنین از شما مخاطبین عزیز سایت همیارپروژه دعوت می کنم که برای انجام پروژه متلب خود آموزش های ما را دنبال نمایید.

نویسنده: زهرا رستمی